Victor Lefèvre (CV)
Adjunct Assistant Professor of Mechanical Engineering
McCormick School of Engineering and Applied Science
Northwestern University
2137 Tech Drive — Catalysis 326 (map)
Evanston, IL 60208-3109
Tel: (847) 491-4322
Email: victor.lefevre@northwestern.edu
I’m passionate about science and technology with a particular interest in how mathematical and computational methods allow us to describe, understand, and predict the world around us.
In my research, I apply these methods to the properties of advanced materials, including particulate and fiber-reinforced elastomers, electro/magnetoactive composites, foams… I also enjoy sharing this vision and passion with my students in my courses on these materials or on other topics.
Research
Research interests
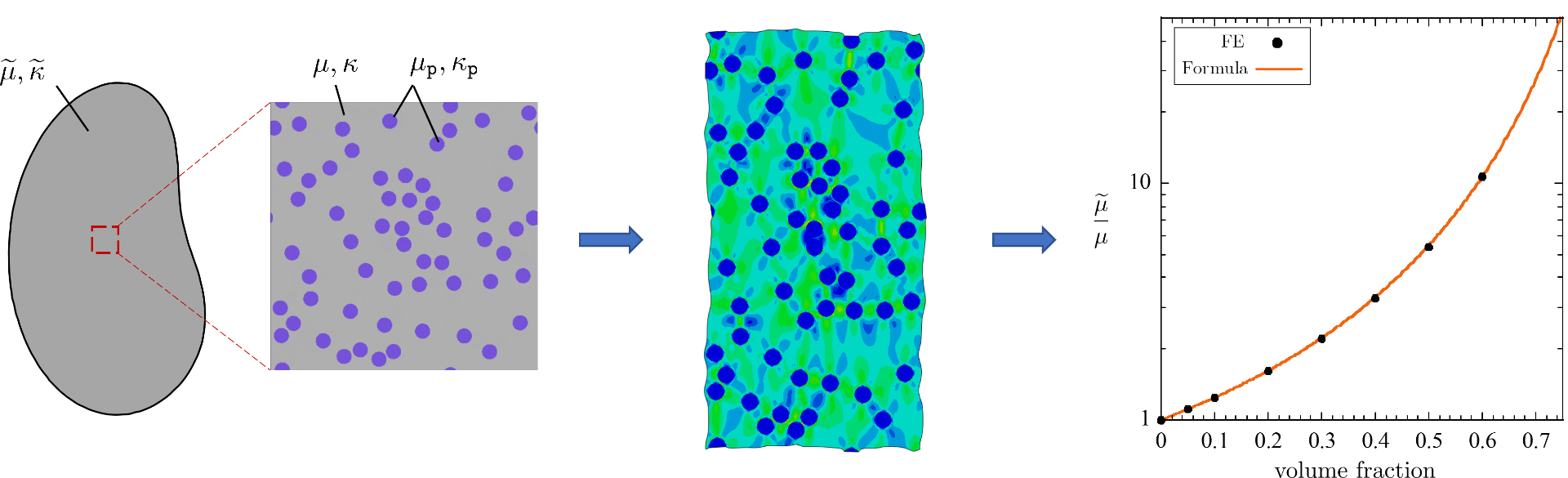
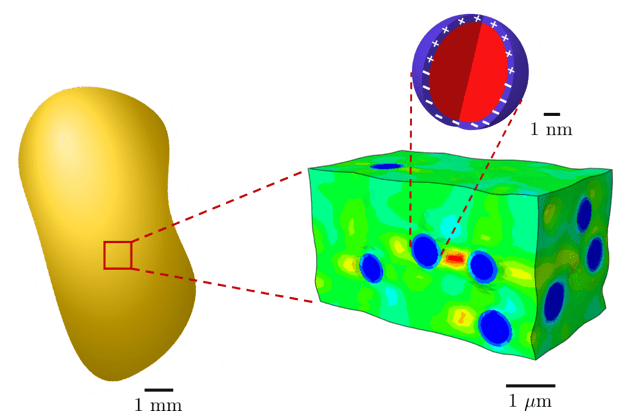 I am interested in highly-deformable heterogeneous materials and the wide range of mechanical and physical properties they exhibit. My research focuses on the development of analytical and computational tools aimed at describing and predicting the macroscopic multi-physics behavior of these materials from their microscopic characteristics. Thanks to their capability to undergo very large deformations in response to a wide range of external stimuli (including, for instance, mechanical, electric, magnetic, or chemical stimuli), these soft smart materials hold tremendous potential for practical uses in new high-end technologies in significant fields such as robotics and medicine.
I am interested in highly-deformable heterogeneous materials and the wide range of mechanical and physical properties they exhibit. My research focuses on the development of analytical and computational tools aimed at describing and predicting the macroscopic multi-physics behavior of these materials from their microscopic characteristics. Thanks to their capability to undergo very large deformations in response to a wide range of external stimuli (including, for instance, mechanical, electric, magnetic, or chemical stimuli), these soft smart materials hold tremendous potential for practical uses in new high-end technologies in significant fields such as robotics and medicine.
Publications
Journal Articles:
J18. Ghosh, K., Lefèvre, V., Lopez-Pamies, O. 2023. The effective shear modulus of a random isotropic suspension of monodisperse liquid n-spheres: From the dilute limit to the percolation threshold. Soft Matter 19, 208–224. (pdf file)
J17. Ghosh, K., Lefèvre, V., Lopez-Pamies, O. 2023. Homogenization of elastomers filled with liquid inclusions: The small-deformation limit. The Special Issue in Recognition of the 85th Birthday of Roger Fosdick. Journal of Elasticity. In press. (pdf file)
J16. Lefèvre, V., Francfort, G.A., Lopez-Pamies, O. 2022. The curious case of 2D isotropic incompressible Neo-Hookean composites. The Special Issue in Recognition of the 90th Birthday of Millard Beatty. Journal of Elasticity 151, 177–186. (pdf file)
J15. Lefèvre, V., Lopez-Pamies, O. 2022. The effective shear modulus of a random isotropic suspension of monodisperse rigid n-spheres: From the dilute limit to the percolation threshold. Extreme Mechanics Letters 55, 101818. (pdf file)
J14. Lefèvre, V. 2020. Electroelastic response of isotropic dielectric elastomer composites with deformation-dependent apparent-permittivity matrix. Journal of Applied Mechanics 87(9), 091006. (pdf file)
J13. Lefèvre, V., Danas, K., Lopez-Pamies, O. 2020. Two families of explicit models constructed from a homogenization solution for the magnetoelastic response of MREs containing iron and ferrouid particles. International Journal of Non-Linear Mechanics 119, 103362. (pdf file)
J12. Lefèvre, V., Garnica, A., Lopez-Pamies, O. 2019. A WENO finite-difference scheme for a new class of Hamilton-Jacobi equations in nonlinear solid mechanics. Computer Methods in Applied Mechanics and Engineering 349, 17–44. (pdf file)
J11. Kothari, M., Cha, M.-H., Lefèvre, V., Kim, K.-S. 2019. Critical curvature localization in graphene. II. Nonlocal flexoelectricity-dielectricity coupling. Proceedings of the Royal Society A. 475, 20180671. (pdf file)
J10. Shrimali, B., Lefèvre, V., Lopez-Pamies, O. 2019. A simple explicit homogenization solution for the macroscopic elastic response of isotropic porous elastomers. Journal of the Mechanics and Physics of Solids 122, 364–380. (pdf file)
J9. Lefèvre, V., Danas, K., Lopez-Pamies, O. 2017. A general result for the magnetoelastic response of isotropic suspensions of iron and ferrofluid particles in rubber, with applications to spherical and cylindrical specimens. Journal of the Mechanics and Physics of Solids 107, 343–364. (pdf file)
J8. Lefèvre, V., Lopez-Pamies, O. 2017. Homogenization of elastic dielectric composites with rapidly oscillating passive and active source terms. SIAM Journal on Applied Mathematics 77, 1962–1988. (pdf file)
J7. Poulain, X., Lefèvre, V., Lopez-Pamies, O., Ravi-Chandar, K. 2017. Damage in elastomers: Nucleation and growth of cavities, micro-cracks, and macro-cracks. International Journal of Fracture 205, 1–21. (pdf file)
J6. Lefèvre, V., Lopez-Pamies, O. 2017. Nonlinear electroelastic deformations of dielectric elastomer composites: II — Non-Gaussian elastic dielectrics. Journal of the Mechanics and Physics of Solids 99, 438–470. (pdf file)
J5. Lefèvre, V., Lopez-Pamies, O. 2017. Nonlinear electroelastic deformations of dielectric elastomer composites: I — Ideal elastic dielectrics. Journal of the Mechanics and Physics of Solids 99, 409–437. (pdf file)
J4. Lefèvre, V., Lopez-Pamies, O. 2015. The overall elastic dielectric properties of fiber-strengthened/weakened elastomers. Journal of Applied Mechanics 82(11), 111009. (pdf file)
J3. Spinelli, S.A., Lefèvre, V., Lopez-Pamies, O. 2015. Dielectric elastomer composites: A general closed-form solution in the small-deformation limit. Journal of the Mechanics and Physics of Solids 83, 263–284. (pdf file)
J2. Lefèvre, V., Ravi-Chandar, K., Lopez-Pamies, O. 2015. Cavitation in rubber: an elastic instability or a fracture phenomenon? International Journal of Fracture 192, 1–23. (pdf file)
J1. Lefèvre, V., Lopez-Pamies, O. 2014. The overall elastic dielectric properties of a suspension of spherical particles in rubber: An exact explicit solution in the small-deformation limit. Journal of Applied Physics 116, 134106. (pdf file)
Subroutines
- UHYPER_Lefevre_Lopez-Pamies: This ABAQUS UHYPER subroutine implements the hyperelastic model for isotropic incompressible filled elastomers (accounting for hydrodynamic, interphasial, and occluded rubber effects) introduced in Lefèvre, V., Lopez-Pamies, O. 2017. Nonlinear electroelastic deformations of dielectric elastomer composites: II — Non-Gaussian elastic dielectrics. Journal of the Mechanics and Physics of Solids 99, 438–470.
- UHYPER_Lefevre_Lopez-Pamies_Liquid_inclusions: This ABAQUS UHYPER subroutine implements the hyperelastic model for isotropic incompressible elastomers filled with liquid-like inclusions introduced in Lefèvre, V., Lopez-Pamies, O. 2017. Nonlinear electroelastic deformations of dielectric elastomer composites: II — Non-Gaussian elastic dielectrics. Journal of the Mechanics and Physics of Solids 99, 438–470.
- UHYPER_Shrimali_Lefevre_Lopez-Pamies: This ABAQUS UHYPER subroutine implements the hyperelastic model for isotropic porous elastomers introduced in Shrimali, B., Lefèvre, V., Lopez-Pamies, O. 2019. A simple explicit homogenization solution for the macroscopic elastic response of isotropic porous elastomers. Journal of the Mechanics and Physics of Solids 122, 364–380. Additional information about this subroutine and examples can be found in the article posted in the SIMULIA Learning Community.
Teaching
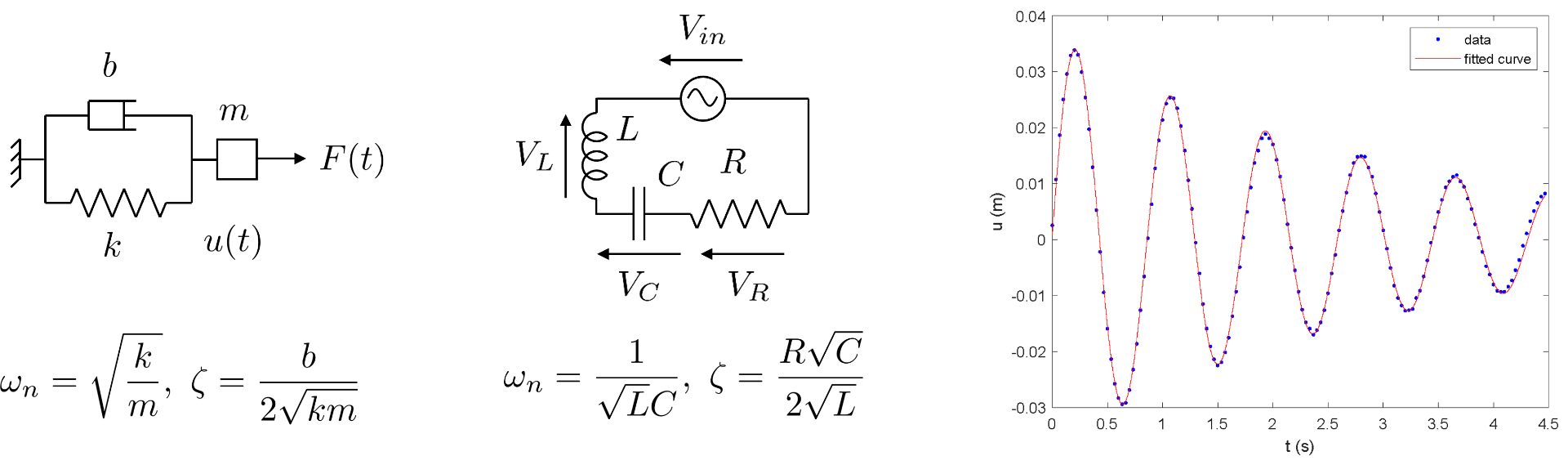
EA3: System dynamics
This course covers the fundamentals of modeling the dynamic response of mechanical and electrical systems described by linear constitutive laws.
Course Outline:
- Linear ordinary differential equations
1st order, 2nd order scalar ODEs, systems of 1st order ODEs, Euler’s method - Mechanical systems
Mechanical components (springs, masses, dampers, external forces), response of simple systems with or without external excitation. - Electrical systems
Electrical components (capacitors, inductors, resistors, power sources), electronic–hydraulic analogy, response of simple systems with or without external excitation. - Analogous systems
Mechanical/Electrical analogies, pendulum, torsional/structural analogies.
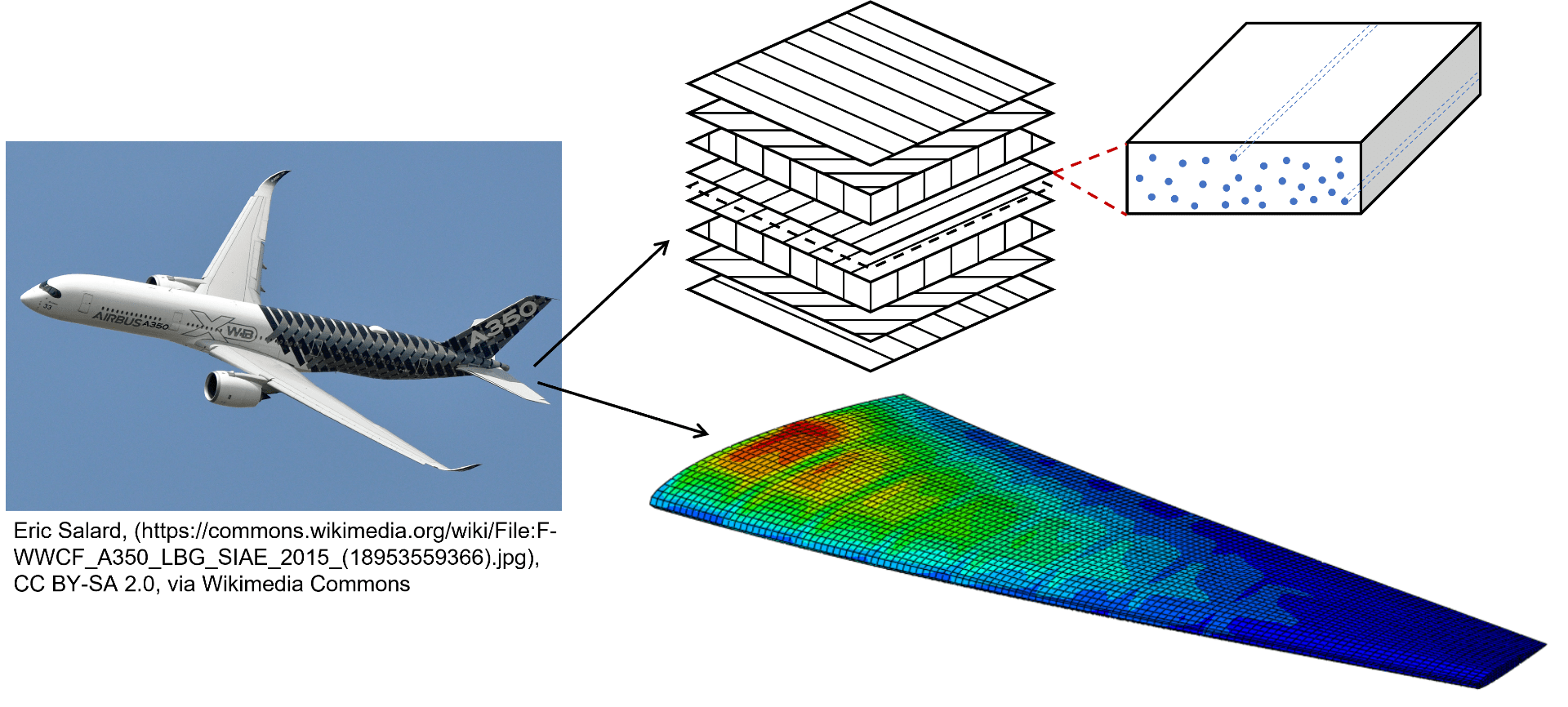
ME414: Mechanics of Composite Materials
This course focuses on the elastic properties of a wide range of composites (laminated materials, particulate/fiber-reinforced composites, multidirectional laminates). It covers a number of engineering methods for the computation of the effective properties of these materials based on the properties and spatial arrangement (volume fraction, shape, orientation, …) of their underlying constituents.
Course Outline:
- Introduction
Basic concepts, Materials, Processes - Elastic behavior of deformable solids
Isotropic/Anisotropic Elasticity - Elastic properties of laminated composites
Laminated composite materials, beams, and plates - Hygrothermal effects
Governing equations, Hygrothermoelastic stress analysis - Failure of laminated composites
Failure criteria, Laminated plate analysis - Elastic properties of composite materials
Particulate composites, Unidirectional fiber-reinforced composites
ME495: Theory of Heterogeneous Solids
This course covers classical and more recent analytical and numerical methods for the computation of various physical properties (viscous/thermal/dielectric, elastic, viscoelastic, thermoelastic, piezoelectric, electrostrictive) of heterogeneous materials that exhibit (non)linear and/or coupled behaviors.
Course Outline:
- Introduction
Review of Continuum Mechanics, Problem description and setting, Classical Voigt and Reuss bounds - 2-scale asymptotic expansion
Composites with periodic microstructures, Unit-cell Finite Element Method - Construction of solutions for exact microstructures
Checkerboards, Laminated materials, Coated assemblages, Iterated dilute homogenization - Comparison medium methods
Eshelby inclusion problem, Hashin-Shtrikman variational principles and bounds, Self-consistent estimates - Beyond linear elastic composites
Viscoelastic composites, Hyperelastic composites, Thermoelastic composites, Elastic dielectrics
ME495: Constitutive Modeling of Soft Materials
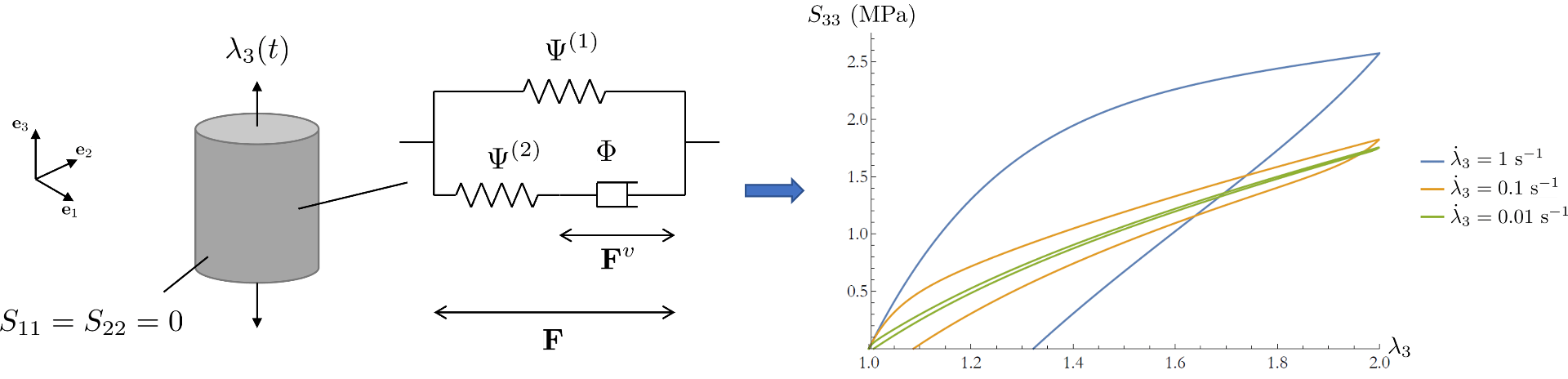 This course covers theoretical frameworks that describe and govern the response of this class of materials within the context of hyperelasticty, hyperviscoelasticity, and finite thermoelasticity.
This course covers theoretical frameworks that describe and govern the response of this class of materials within the context of hyperelasticty, hyperviscoelasticity, and finite thermoelasticity.
Course Outline:
- Introduction
Tensor algebra, tensor calculus, kinematics - Balance principles (I)
Balance laws, 1st and 2nd law of Thermodynamics - Constitutive modeling
Two-potential framework, Hyperelasticity, Hyperviscoelasticity, Finite thermoelasticity - Balance principles (II)
Configurational forces and phase transitions, Fracture, Soft hydrogels
Last Updated: 08/24/2022